A method for traction ability research of rover wheels on mixed planet terrain with movable stones

The Chang’e-6/7/8 exploration mission has been announced officially by China recently, and the international lunar and Mars research station plans will be carried out within the 2030s. It can be predicted that China’s future lunar and Mars surface exploration activities will last longer, have a larger exploration range, and have a more complex terrain to traverse and explore, which will pose severe challenges to the working performance of the planet rover and its adaptability to the planet surface environment.

One of the key problems will be to study the relationship between the mechanical properties of planet soil and the traction performance of the planet rover’s wheels. The mixed terrains of terramechanics research are mainly composed of static stones and loose soil.

Whereas, the movement behavior of stones is often ignored while analyzing the influence of the wheel’s traction performance caused by mixed terrain. Since the existing theory explaining the terramechanics problem of the planetary vehicle’s wheel moving in the mixed terrain of movable stones and loose soil is imperfect and its calculation is relatively complex, the new solution of contact force of the wheel of a planetary rover under the mixed terrain of a movable stone and loose soil is worthy of research.

In a research paper recently published in Space: Science & Technology, Jiangshan Du and Tieqiu Huang, from Beijing Jiaotong University, aiming at these problems, propose a residual soil model for solving the interaction force between the remaining soil that is not covered by stones and wheel and a plastic homogeneous soil mechanics model to calculate the soil force supplied to a movable stone.

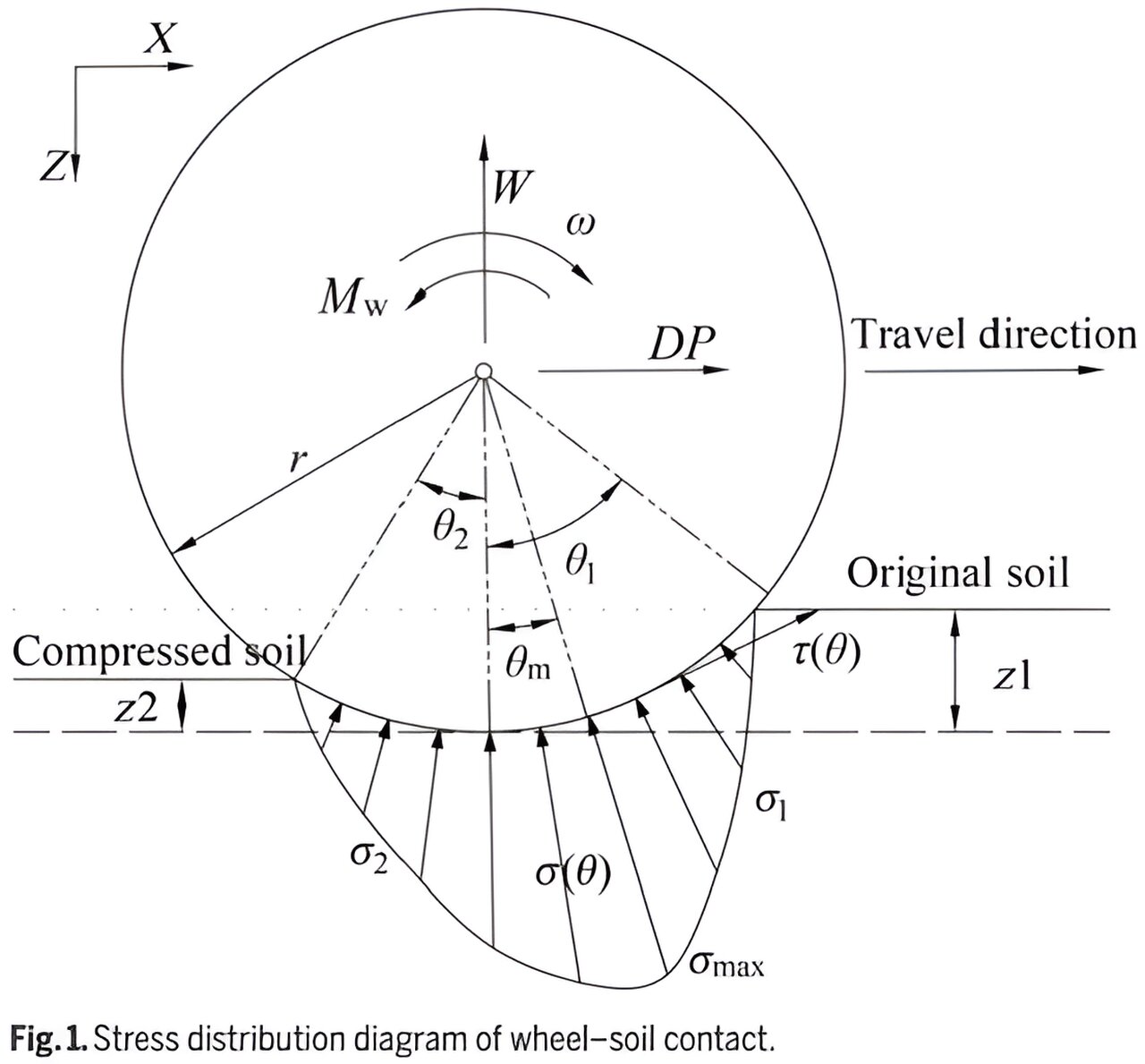
First, the authors review two typical interaction model between wheel and ground. In the Wong–Reece model and the Janosi model, the contact between rigid wheel and soft soil is shown. The Wong–Reece model describes the relation between the angle of approach Θ₁ and the sinkage z for given μ value which is determined by experiments.

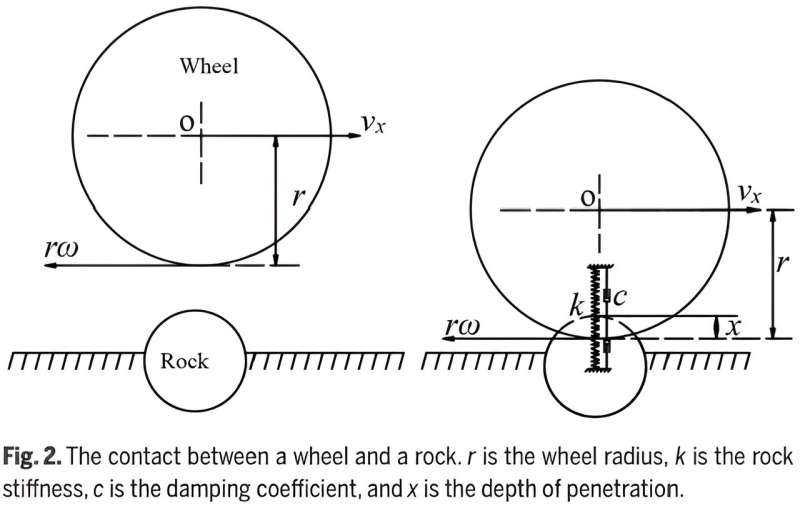
The Janosi shear stress model formulates τ(Θ) under μ =1. They two together result in the supporting force W and the drawbar pull DP via integrations. In the contact model of a rigid wheel and stone, the nonlinear spring-damper model based on the Hertz contact theory is adopted to calculate the normal force between a solid and a solid.

When a wheel runs across a stone, it also produces adhesion P calculated by the Coulomb friction model and resistance moment M_w.

Then, the authors elaborate two proposed models. The proposed models meet the following assumptions: 1) The models occur on the mixed terrain with a movable stone and the loose soil; 2) there is no contact between stones, no matter whether the stones move or not; 3) ignoring the lateral force, the models are only used on the 2-dimensional plane.

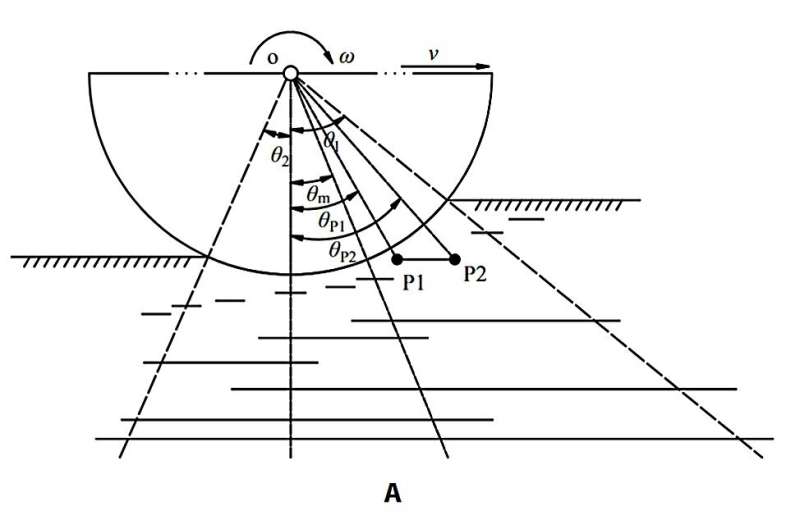
In residual soil model, the basic idea is to modify the integration area for W and DP to solve the interaction force between the wheel and remaining soil, when a moving wheel is in contact with a stone and soil at the same time. Under this condition, a wheel passing through a stone is regarded as the process through which a stone successively passes through the angle of approach Θ₁, the angle of maximum stress Θ_m, and the angle of departure Θ₂.

Eventually, it leaves the area where a wheel interacts with soil. In the plastic homogeneous soil mechanics model, Bekker’s pressure-sinkage model, which reflects the bearing properties of soil and can be approximately regarded as a typical nonlinear spring model, can be further extended to 2-dimensional space to research the relationships between pressure and sinkage in 2 directions.

Last, the authors carry out the simulation and the experiment to verify the proposed models. Wheel width is 14 cm. The wheel’s diameter is 30 cm. The forward speed of the wheel is 0.03 m/s. The slip ratio is 0.3. The wheel is a uniform rectilinear motion along the positive X axis. In experiment, the traveling motor 4 outputs moment to the wheel via a belt conveyor to push the wheel forward while another driving motor 4 located below relies on a coupling to make the wheel rotate around its axis.

The traveling and rotating speeds are measured by the encoders 3 connected to the drive shafts. This study takes the Martian soil as the research object; thus, dry sand is selected as the soil and the topography is flat. The validity of the plastic homogeneous soil mechanics model and the residual soil model is verified by comparing the traction performance error of the rigid wheel in contact with different rocks in simulation and experiment.

The results show the following: 1) For the movable stones, the simulation results of sinkage, drawbar pull, and resistance moment are in good agreement with the experimental results, which verifies the effectiveness of the above-proposed models; 2) Compared with the fixed stone, it is distinct that the movement states of stones have an important impact on the wheel’s traction performance. In some cases, ignoring the influence of the stone movement on the wheel traction ability, therefore, may lead to large errors.