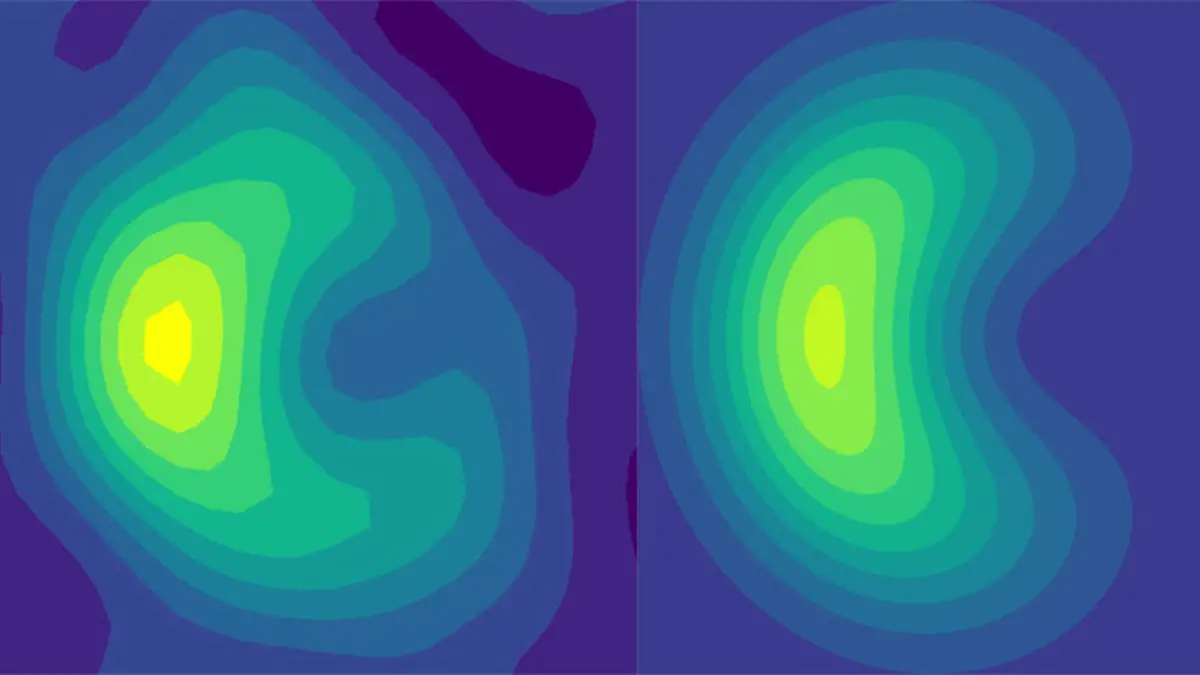
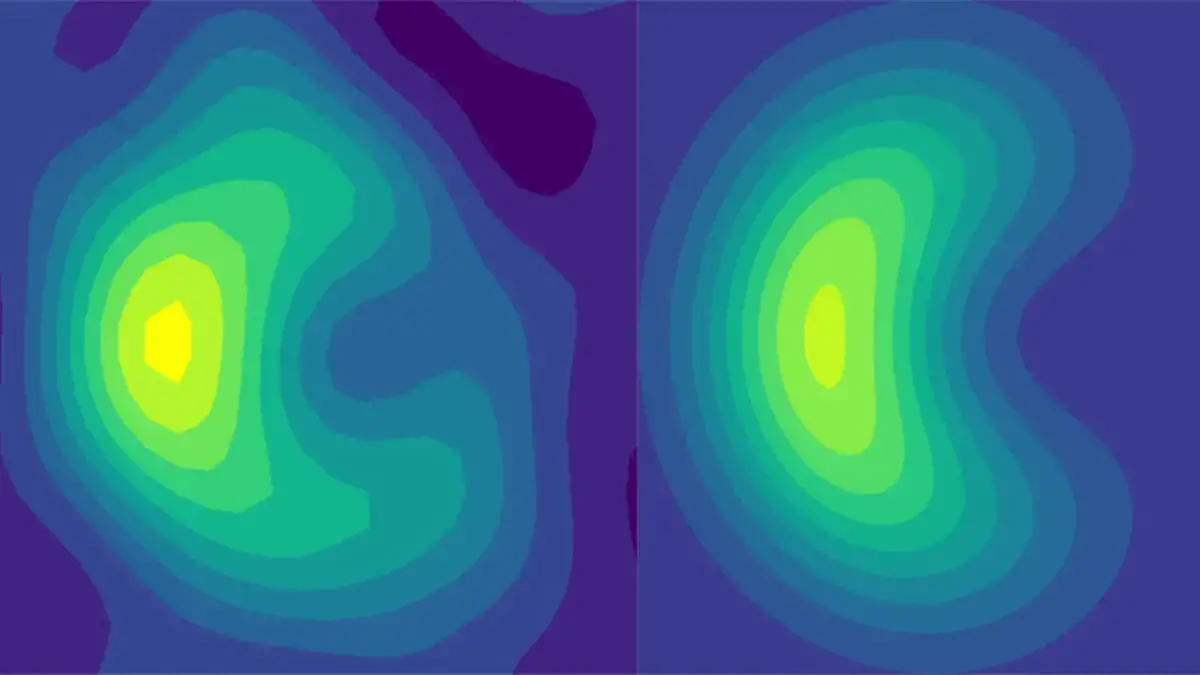
Experimental results from a quantum computer (left) that match well with theory (right) are the first quantum-based method to show a quantum effect in the way light-absorbing molecules interact with incoming photons. Credit: Jacob Whitlow, Duke University
A quantum computer slowed simulated molecular quantum effects by a billion times, allowing researchers to directly measure them for the first time.
Researchers at Duke University have implemented a quantum-based method to observe a quantum effect in the way light-absorbing molecules interact with incoming photons. Known as a conical intersection, the effect puts limitations on the paths molecules can take to change between different configurations.
The observation method makes use of a quantum simulator, developed from research in quantum computing, and addresses a long-standing, fundamental question in chemistry critical to processes such as photosynthesis, vision, and photocatalysis. It is also an example of how advances in quantum computing are being used to investigate fundamental science.
The results were published on August 28 in the journal Nature Chemistry.
Conical Intersections
“As soon as quantum chemists ran into these conical intersection phenomena, the mathematical theory said that there were certain molecular arrangements that could not be reached from one to the other,” said Kenneth Brown, the Michael J. Fitzpatrick Distinguished Professor of Engineering at Duke. “That constraint, called a geometric phase, isn’t impossible to measure, but nobody has been able to do it. Using a quantum simulator gave us a way to see it in its natural quantum existence.”
Conical intersections can be visualized as a mountain peak touching the tip of its reflection coming from above and govern the motion of electrons between energy states. The bottom half of the conical intersection represents the energy states and physical locations of an unexcited molecule in its ground state. The top half represents the same molecule but with its electrons excited, having absorbed energy from an incoming light particle.
The molecule can’t stay in the top state — its electrons are out of position relative to their host atoms. To return to the more favorable lower energy state, the molecule’s atoms begin rearranging themselves to meet the electrons. The point where the two mountains meet —the conical intersection — represents an inflection point. The atoms can either fail to get to the other side by readjusting to their original state, dumping excess energy in the molecules around them in the process, or they can successfully make the switch.
Quantum Effects in Molecules
Because the atoms and electrons are moving so fast, however, they exhibit quantum effects. Rather than being in any one shape — at any one place on the mountain — at any given time, the molecule is actually in many shapes at once. One could think of all these possible locations as being represented by a blanket wrapped around a portion of the mountainous landscape.
However, due to a mathematical quirk in the system that emerges from the underlying mathematics, called a geometric phase, certain molecular transformations can’t happen. The blanket can’t wrap entirely around the mountain.
“If a molecule has two different paths to take to get to the same final shape, and those paths happen to surround a conical intersection, then the molecule wouldn’t be able to take that shape,” said Jacob Whitlow, a doctoral student working in Brown’s laboratory. “It’s an effect that’s hard to gain intuition for, because geometric phase is weird even from a quantum mechanical standpoint.”
Challenges of Measuring Geometric Phase
Measuring this quantum effect has always been challenging because it is both short-lived, on the order of femtoseconds, and small, on the scale of atoms. And any disruption to the system will prevent its measurement. While many smaller pieces of the larger conical intersection phenomenon have been studied and measured, the geometric phase has always eluded researchers.
Quantum Computers in Research
“If conical intersections exist — which they do — then the geometric phase has to exist,” said Brown, who also holds appointments in Duke physics and chemistry. “But what does it mean to say something exists that you can’t measure?”
In the paper, Whitlow and coworkers used a five-ion quantum computer built by the group of Jungsang Kim, the Schiciano Family Distinguished Professor of Electrical and Computer Engineering at Duke. The quantum computer uses lasers to manipulate charged atoms in a vacuum, providing a high level of control. Whitlow and Zhubing Jia, a PhD student in Brown’s laboratory, also expanded the capability of the system by developing ways to physically nudge the floating ions within their electromagnetic traps.
Based on how the ions are moved and the quantum state that they’re placed in, they can fundamentally exhibit the exact same quantum mechanisms as the motion of atoms around a conical intersection. And because the quantum dynamics of the trapped ions are about a billion times slower than those of a molecule, the researchers were able to make direct measurements of the geometric phase in action.
The results look something like a two-dimensional crescent moon. As depicted in the conical intersection graph, certain configurations on one side of the cone fail to reach the other side of the cone even though there is no energy barrier. The experiment, Brown says, is an elegant example of how even today’s rudimentary quantum computers can model and reveal the inner quantum workings of complex quantum systems.
“The beauty of trapped ions is that they get rid of the complicated environment and make the system clean enough to make these measurements,” said Brown.
An independent experiment at the University of Sydney, Australia has also observed the effects of the geometric phase using an ion trap quantum simulator. The approach differs in many technical details, but the overall observations are consistent. The Sydney work will be published in the same issue of Nature Chemistry.
Reference: “Simulating Conical Intersections with Trapped Ions” by Jacob Whitlow, Zhubing Jia, Ye Wang, Chao Fang, Jungsang Kim and Kenneth R. Brown, 28 August 2023, Nature Chemistry.
DOI: 10.1038/s41557-023-01303-0
This work was supported by Intelligence Advanced Research Projects Activity (W911NF-16-1-0082), the National Science Foundation (Phy-1818914, OMA-2120757), the Department of Energy Office of Advanced Scientific Computing Research QSCOUT program (DE-0019449), and the Army Research Office (W911NF-18-1-0218).