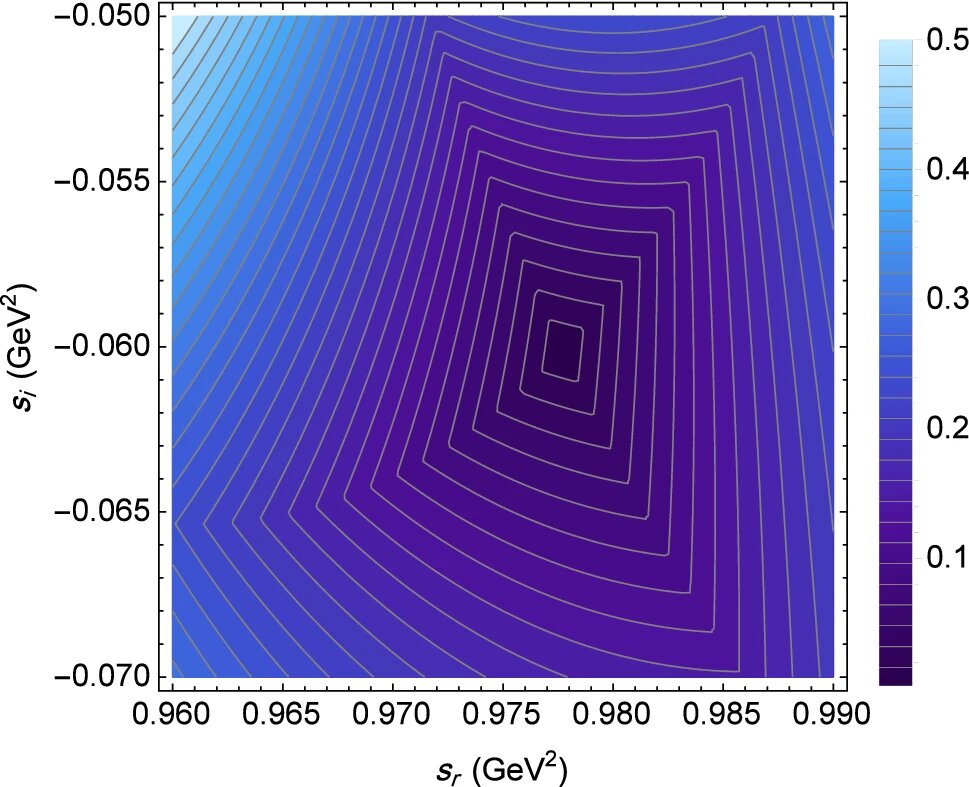
![Contour plot of function F(sr,si) [defined in (55)]. The point at which F=0 represents the first physical isovector scalar meson pole and provides the properties of the a0(980). Credit: The European Physical Journal C (2022). DOI: 10.1140/epjc/s10052-022-11103-4 Advances in understanding the quark substructure of scalars](https://skynews.icu/wp-content/uploads/2022/12/Advances-in-understanding-the-quark-substructure-of-scalars.jpg)
At this stage in the evolution of the universe (about 14 billion years after the big bang) there are four fundamental forces in action that cause interactions among the constituents of matter.
One of these forces is gravity that, for example, keeps us revolving around the sun and be able to enjoy the four seasons. Another one is the electromagnetic force that benefits us every day. From the light bulb that we turn on every night to the dynamics of electrons inside our electronic devices, they are all driven by the electromagnetic force. The other two forces are not as commonly noticed in daily life, but this does not mean that they are any less important.
These two forces are confined within the nucleus of atoms (distances around 10-15 m or smaller) and are traditionally referred to as “nuclear forces.” One of them is the strong nuclear force (the strongest of all four forces) that is responsible for keeping the nucleus intact by bonding its protons and neutrons together.
Without the strong nuclear force, nuclei wouldn’t form, we wouldn’t exist, and the sky would be empty. The other one is the weak nuclear force that is responsible for transforming one nucleus into another and sometimes breaking them apart. We benefit from the effects of the weak nuclear force in our nuclear reactors.
The protons and neutrons are members of a large family of composite particles called hadrons, and they are all made of fundamental particles called quarks. The theory that describes the strong interaction of quarks is called Quantum Chromodynamics (QCD), according to which, the quarks engage in strong interaction by exchanging mediating particles called gluons.
This is similar to how fundamental charged particles engage in electromagnetic interaction by exchanging photons in the theory of Quantum Electrodynamics (QED). However, there are some major differences between QCD and QED, such as, for example, the fact that photons cannot form bound states but gluons, in principle, can bound together and form composites called glueballs.
Theoretical understanding of the formation and interactions of glueballs with quark matter, as well as their experimental detection, are ambitious objectives of formidable complexity. Despite several Nobel prizes in physics already awarded for the remarkable discoveries in particle physics related to QCD, some aspects remain open questions and have challenged the theoretical physics for many decades. This problem is recognized by the Clay Mathematics Institute (www.claymath.org) as one of the seven unsolved problems in mathematics, known as Millennium Problems in Mathematics.
The main research of Amir Fariborz is on the strong interaction of quarks and their interactions with glueballs. Models developed by Fariborz and collaborators have been widely successful in describing experimental data and received noticeable citations in the literature. Further information about Fariborz’s research can be found at the Inspire high energy physics literature database.
In this recent paper published in The European Physical Journal C the generalized linear sigma model of QCD (developed by Fariborz et al) is applied to the scattering of two special types of hadrons called pion (π) and eta (η). This scattering is particularly important because it probes an intermediate composite state [called a0980] which is part of a family of hadrons called scalar mesons.
These composite particles of quarks play a special role in QCD by breaking a symmetry in the dynamical equations called chiral symmetry. Understanding the quark substructure of scalars sheds light on the strong interaction of quarks and gluons. This recent work has confirmed that the light scalar mesons contain a significant four-quark component, a feature that puts scalar mesons in the challenging category of exotic hadron spectroscopy.
More information:
Amir H. Fariborz et al, Chiral nonet mixing in pi-eta scattering, The European Physical Journal C (2022). DOI: 10.1140/epjc/s10052-022-11103-4
Provided by
Suny Polytechnic Institute
Citation:
Advances in understanding the quark substructure of scalars (2022, December 23)
retrieved 23 December 2022
from https://phys.org/news/2022-12-advances-quark-substructure-scalars.html
This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no
part may be reproduced without the written permission. The content is provided for information purposes only.