Preventing errors of reasoning in medicine and law

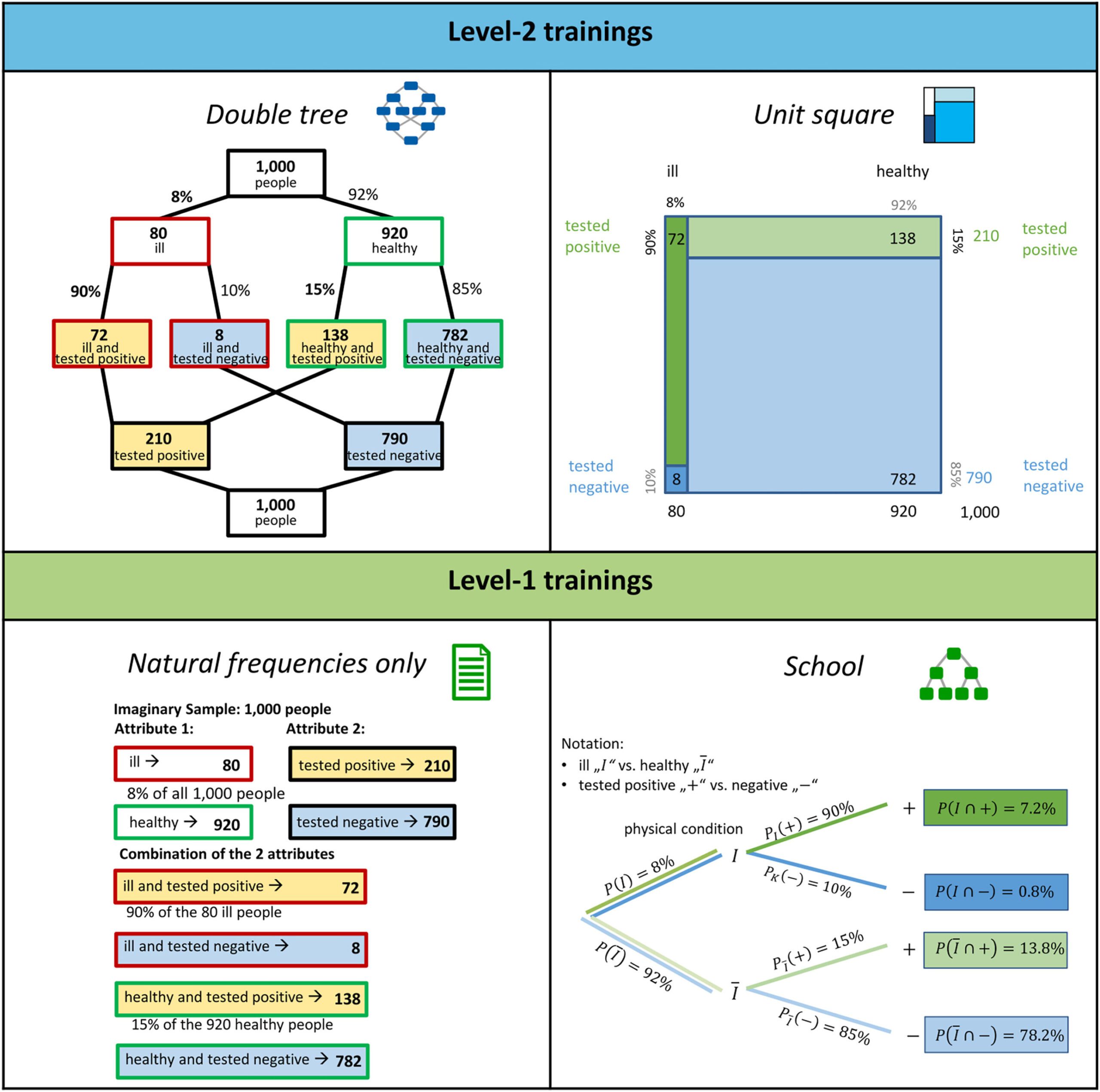
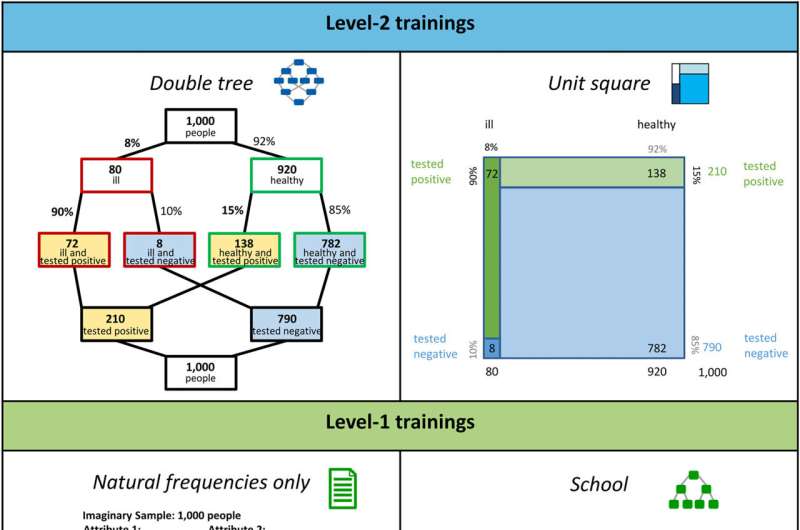
How trustworthy is a positive HIV test result? How probable is an actual infection when the test is positive? Even professionals often get such questions wrong, which can lead to misdiagnoses and unnecessary surgeries.

In a new study with medicine and law students, a team of mathematics education scholars from the Universities of Regensburg, Kassel, and Freiburg, Heidelberg University of Education, and LMU Munich has compared four different training courses designed to help students gain a better understanding of probabilities.

The findings of the German Research Foundation project TrainBayes have now been published in the journal Learning and Instruction.

The focus was on so-called Bayesian situations. An example: Let’s say that at a certain point during the coronavirus pandemic, 0.1% of the population was infected with SARS-CoV-2. Then one person carries out a SARS-CoV-2 self-test. 96% of infected people receive a positive test result. However, 2% of non-infected people also get a positive test result. What does this mean? How likely is it that the person in question is actually infected if they get a positive test result?

“Many people—even experts in the respective domains—significantly overestimate this probability,” says LMU mathematics educationalist Karin Binder, one of the authors of the study. “The positive parameters of the tests cause people to trust the test result and overlook the small proportion of infected people.”

To illustrate this situation, we can imagine that 100,000 people have been tested: Only, say, 100 people are infected, of which 96 receive a positive result. Of the 99,900 healthy people, 2%—that is, 1,998—also receive a positive result. Consequently, of the 2,094 people in total with positive test results, only 96 are actually infected—corresponding to almost 5%. As such, a positive test result is not yet, by itself, cause for alarm.

Nicole Steib from the University of Regensburg, lead author of the study, explains, “The translation of probabilities (2%) into concrete frequencies (1,998 out of 99,900), combined with representation of the information in a double tree, proved to be the most effective method of helping students solve similar tasks.”

The probability trees generally used in schools, by contrast, only help students with particularly advanced prior mathematical knowledge. In a follow-on project, the new training approaches are to be integrated into lessons for teaching at school.